Dynamically Generating PRNG Functions
by Ethan Alexander Shulman (March 22, 2024)

Pseudorandom number generator(PRNG) functions are notoriously difficult to create, even the standard C rand() function is known to be predictable and shows patterns. This is because rand() is implemented using a fast and simple PRNG known as a linear congruential generator, if you look at the code (a*b+c)%d it's pretty easy to see why it's predictable. It will always fall into a repeating period with varying gaps depending on b/d, you can see these periods as planes when you run a spectral test. Certain b/d values produce decent pseudorandomness but how do you find them? This is a challenge with most PRNG techniques, a lot of the randomness comes from the constant values in your operations. My procedure is to automate finding these values using a simple brute force search, randomly generate values and then test to see if they fail randomness tests. But why stop at operand values, why not randomly generate the code and operations as well? In this post I'm going to cover randomly generating PRNG functions and testing them for randomness.

Article sections:
Meta Programming
Visualization
Random Lookups
Statistical Testing
Automation
Code

Meta Programming
I will be using Javascript for all the programming, it will make everything easy we can dynamically compile code with eval, display visualizations with canvas, run our tests in WebWorkers and interface with the code using the console. Our PRNG function will be uint32 based to take advantage of overflow wrapping and binary arithmetic. The function will take in a non-random seed and output a pseudorandom value of the same size. We're going to jump straight ahead into the Javascript with a simple text HTML page wrapping it. Create a new HTML file, I've named mine 'PRNGG.html', open it in a text editor and paste in the code below. Looking at the GenPRNG function we have an array of operations and we randomly select them to build the code. Each operation has random operand values to go along with them, the code and values are stored in prngCode that is then converted to Javascript. In the generated code the PRNG state, including input seed and output hash, is stored in a single buffer ubuf. There is also tbuf a temporary buffer specifically for Javascript. In Javascript you need a Uint32Array to do uint32 operations so we use tbuf, in C or another language you would just declare a uint32 variable.

I want to dynamically generate PRNG function code but if we use completely random operations it will generate mostly garbage. Because of this I'm going to write a few specific 'PRNG operations' which are designed to converge towards pseudorandomness. If you look at different hash functions like FNV or SHA some of the most occuring arithmetic is xor, multiplication and bitshifting. Xor is essential it will be used to fold bits together allowing us to stack the effects of operations and when bitshifting it will fill in the empty spaces where 0s were shifted in. Multiplication is a powerful operation for PRNG and cryptography, with the right operands it can cause input bits to spread across the output. Even if our input seed has only a few bits set we want them to spread across the output pseudorandomly effecting all the output bits. For our first PRNG operation were going to use the tried and tested multiply bitshift. Add this code to the switch statement in ToCodeJavascript.
With that we have a basic PRNG, were going to go ahead and generate some random numbers with it. Open up the HTML file in a browser and bring up the console(F12/Developer Tools), run the following code to generate a PRNG and print some of its output values. I got the output 0, 403796891, 537740343, 3339768201, 944534558, 4088418448, 2218018289, 1929476160, 2596031549, 1594184361. Seems random but looking at the individual numbers as text isn't a good way of recognizing patterns.

Visualization
In the start of the article I mentioned the spectral test, plotting the random values in a 2D/3D/etc space allows you to see new patterns you may not have in 1D. For example when you have a 100x100 image where id=x+y*100 each unit on the Y appears 1 pixel distance but it's actually 100 units away in the PRNG sequence. Now if a pattern appears every ~100 or so outputs of the PRNG it will show up across the Y axis because the values are now displayed together in lines/planes. So for our first visualization were going to output the PRNG bytes into a grayscale image, add the following function.

1 Multiply	4 Multiplys
		Now we can get a much better idea of what the PRNG function is doing. In the console generate a PRNG with GenPRNG([OP_MULTIPLY],4, 1,1) and visualize it with VisualizeBytes(256,256), it should generate noise. Now try GenPRNG([OP_MULTIPLY],1, 1,1), with only 1 operation you should see band/line patterns across the image. We can already visually see that applying more operations results in more noise.

The one issue with displaying bytes is that the upper bits contribute more to the pixel than lower bits, making it hard to see patterns in the lower bits. To view patterns equally across all the bits we can generate a black and white image for every single bit position. Add the following function.
In the OP_MULTIPLY code you might have noticed the (opId%2===0 ? ">>>16" : "") where it only bitshifts every other operation. We can use VisualizeBits to show why this is done, see the table below.

No Shift	Always Shift	Shift Every Other

With no shifting the noise ends up in the upper bits because multiplying results in bits shifting upwards. But if we shift down everytime no bits will end up in the upper bits, as a form of middle ground we shift every other time. This is a fairly reliable way of distributing the bits uniformly, I also tried random amounts of bitshifts but it's unreliable with a small number of operations. The more operations you have the higher chance the random bitshifts average out, otherwise you get bits shifted too much to one end.

Random Lookups
You can chain together hash functions by seeding the input of one using the output of another, a random lookup of a random function. The rest of our PRNG operations are going to use random lookups to multiply the amount of randomness, especially with a lot of operations. Reading the code before you maybe noticed the argument stateBufSz in GenPRNG, used to set the state buffer size larger than the PRNG size. Having a buffer larger than the PRNG size allows for 'hidden' state values which don't end up in the final output but still contribute to its computation. With OP_MULTIPLY this has a limited effect because it always reads the last state, but if we create operations with random lookups they can take full advantage.

In ToCodeJavascript you can see rbi(state read index) and wbi(state write index), during the loop wbi is incremented and rolls over to 0 once it reaches the end. This creates a circular buffer where PRNG states are temporarily stored until the write index goes over that position again. These positions of previous states which aren't in the final output are the 'hidden' states. To do our random lookup were simply going to take the previous state value and sample the buffer using it as the index. Insert the following code before the switch statement in ToCodeJavascript. All the rest of our operations will use lookups so if the op is greater than OP_MULTIPLY it's a lookup operation. The previous state is modulo'd by the buffer size and used as an index, the value read is stored in tbuf[0] to use in our operation.

Now that we have a random lookup let's create our first lookup operation, bit rotation, a perfect operation for spreading seed bits across the output. While bit rotation is reversible and is not random on its own, combined with a random lookup it's very effective at spreading bits. Add OP_LOOKUP_ROTATE to the enum declaration, insert the case statement in ToCodeJavascript. This rotates the bits of the random lookup value 1-31 places, xor's it with the inverted previous state, and xor's it with the output state. Inverting the previous state isn't essential but it helps even out the ratio of 0/1 bits.

Now let's test out using this new operation, running GenPRNG([OP_LOOKUP_ROTATE],OP_COUNT,1,3) with varying OP_COUNT sizes gives us the following results.

OP_COUNT=1	OP_COUNT=2	OP_COUNT=3	OP_COUNT=6

You can see as you increase operation count it gets progressively noisier, reaching visible noise at 6 operations. OP_LOOKUP_ROTATE requires a few more operations than OP_MULTIPLY which can achieve noise after just 2-3 operations. But that makes sense because bit rotation spreads bits out slower than multiplication.

The next operation will be addition, the rollover from binary addition is decent at spreading bits and it can also seed new 1 bits. If you noticed with OP_MULTIPLY when the seed is 0 the output is always 0, this is because it won't have any 1 bits if the input seed doesn't. Addition can make up for this by introducing new 1 bits into the PRNG state. Add OP_LOOKUP_ADD to the enum declaration, insert the case statement in ToCodeJavascript. The operation adds a random uint32 to the random lookup value, xor's it with the random lookup value right shifted by 1-5 bits, xor's it with the previous state and xor's it with the output state. We need to xor and right bitshift the random lookup value to make up for the bits removed from rolling over during the addition.

Running GenPRNG([OP_LOOKUP_ADD],OP_COUNT,1,3) and visualizing gives us the following.

OP_COUNT=1	OP_COUNT=2	OP_COUNT=3	OP_COUNT=6

Not too different than the bit rotation results, a bit worse though even at 6 operations you can see some distribution issues with more white than black.

The final operation is going to be multiplication again but we will multiply the random lookup instead of the previous state. Add OP_LOOKUP_MULTIPLY to the enum declaration, insert the case statement in ToCodeJavascript.
Visualizing the bits of GenPRNG([OP_LOOKUP_MULTIPLY],OP_COUNT,1,3) we can see that multiplication wins the race to spread bits, achieving visible noise in 4 operations.

OP_COUNT=1	OP_COUNT=2	OP_COUNT=3	OP_COUNT=4

Statistical Testing
The real battle has only just begun, now we must automatically test the quality of our PRNG. Yea sure we have some PRNG functions that look noisy to our human eye but how do we measure this quality of noisiness algorithmically? When we are looking at the visualized bits our eyes are scanning for any pattern, a sequence or correlated events that show up more than normal. Scanning for patterns across images would be very expensive and an indirect way of testing the noise, we only visualize as images for our human eye. As mentioned above in the Visualization section, we convert to images to bring output bytes of large offsets visually together, allowing our human perception to see patterns that would normally be invisible from the large offsets. Well when were scanning algorithmically we don't need to convert to images first, we can just directly sample the varying offsets from a buffer of the PRNG sequence.

Since we aren't scanning 2D images like our human eye we aren't going to be searching for your average geometry. We want to find patterns that appear plainly obvious like lines but we also want to find patterns basically invisible that only exist in 'cracks'. The smallest near invisible patterns only show up as correlation, where you have a pair of bits whose state is related to each other. Nicely enough this property also holds true for the plainly obvious patterns like lines, sequences or shapes. To measure correlated bits we will take the difference(xor) of bits at varying offsets and count their distribution. True white noise should have an even distribution across all offsets, for example if we measure 1000 samples there should be around 500 counts of 0 and 1.

To sample the distribution accurately we will need lots of samples and processing will take some time. We're going to use a WebWorker to run the testing, this way it runs in a separate thread and we can avoid lagging the browser. Let's create a WebWorker, add the following function, this creates a new WebWorker directly from a code string.
The testing process starts pretty simple a for loop that runs the PRNG function and counts the distribution of the output. The more samples and iterations in the loop the less variance in the test results, more iterations higher accuracy. Now first of all we're just going to measure the distribution of the bit states themselves. Loop through all bits in the PRNG output and count up the 1's, we only need to count 1's because count0s = iterations-count1s. Since we can create a WebWorker straight from a string we're going to load the string from a plaintext script element. Add the following code below the existing script element and before style. First we load the test parameters from the WebWorker message evt.data, allocate buffers to count bits and store the previous PRNG outputs. The previous PRNG output is used to measure differences. Inside the testing loop the seed is populated using iter as a uint32 then we run the PRNG function. Loop through all the bits of the output and increment the corresponding counter when we find a 1. Once complete we send the bitCounts array back to the main Javascript thread for analyzing, bitCounts is our array of bit distributions.

Back in the main Javascript code we will now build the WebWorker code and launch the test. Load the worker code as a string using document.getElementById().textContent, prepend code creating ubuf, tbuf and prngFunc. Create the worker and start the test by sending the parameters with postMessage. Insert the variables and function code below.
We're going to try it out with a small test, run the following code in the console. This code generates a 4 operation PRNG, tests it over 10000 iterations and prints the bit distribution to the console. Running it should print an array of 32 integers to the console, one for each bit position, whose values are around 5000.

Back in the TestWorker code we're going to finish up by counting differences between pairs of bits. First we copy the PRNG output into diffBuffer for measuring the differences, then we start the main loop through the offset range up to max(countDiffRange,iter). We clamp the difference range to iter so that diffBuffer isn't read outside what has been written. Next we have 3 more loops, offInt for the uint32 offset, ob for the bit offset and s for the PRNG index. Inside these loops we now have the uint32 indices, indA and indB, that we need to sample from diffBuffer to measure the difference. We sample these values and combine them(via bit rotation) into a single uint32, which is xor'd with our PRNG output. Then it's as simple as repeating our bit counter from before, loop through the 32 bits and count the 1's. Insert this code in the bottom of the testing loop, replacing if !countDiffRange.
That completes our WebWorker code but we're not quite done yet, we need to process the bitCounts array sent back to the main Javascript thread. Whatever onTestDone function you used with TestPRNG will be passed bitCounts via evt.data. We're going to write another function to go through the bit counts and measure the error compared to the expected values. Mentioned earlier say we have 1000 samples the bit counts should be around 500, our expected value is simply iterations/2. In our function we loop through the bit counts, for the bit value counts we take the count and normalize it from 0-200 so the error is in the percent range 0-100. The difference counts are scaled by normScale for a similar reason but also to account for the missed iterations at the start when off=max(countDiffRange,iter) is being limited by iter. We take the maximum of those errors and store them in testValueError and testDiffError. Add the TestError function seen below.
With our testing functions we're now going to test all the operations to see how they measure alone and matched with each other. I've written some code here which will go through the operations, generating many PRNG's and measuring the test results. Download the code, run it in the console to test the operations. Or don't, the tests will take a long time anyways, and you can just look at my graphed results down below.

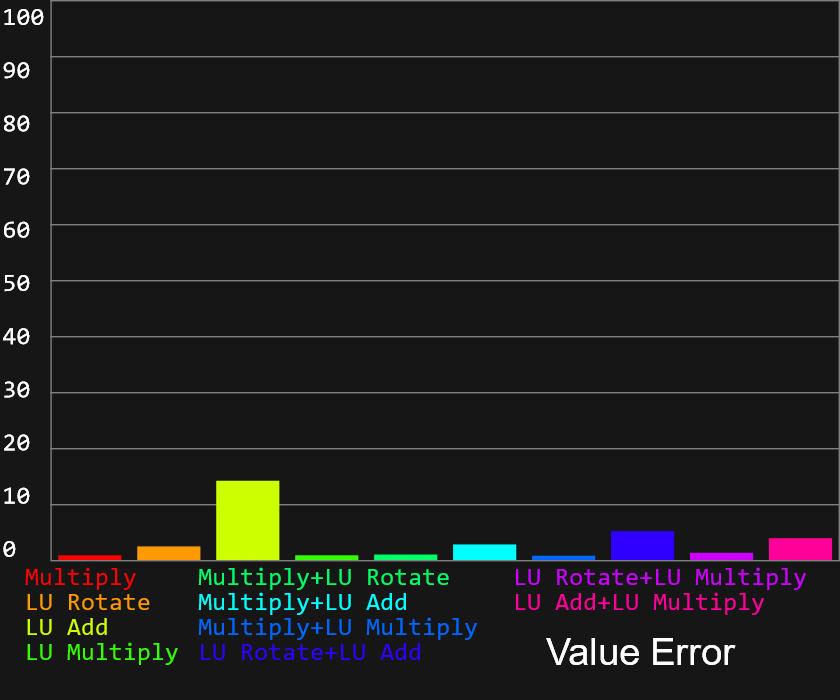
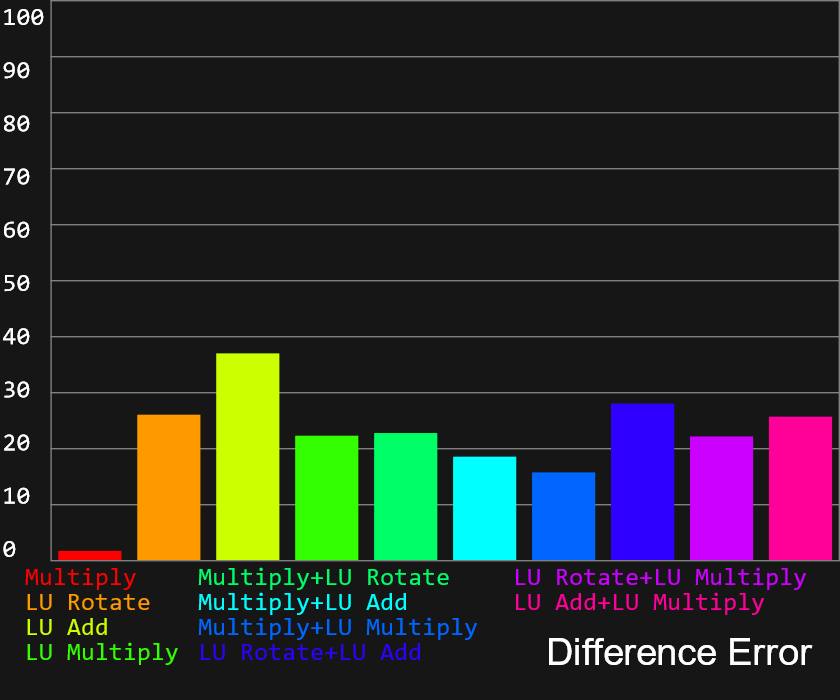These test results are with ITERATIONS = 1e5, TEST_RANGE = 100, GENERATIONS = 100 and OP_COUNT = 3. As OP_COUNT is increased the different options all converge to nearly the same result, I've kept OP_COUNT small to purposefully highlight the difference. The results are mostly unsurprising, multiply is by far the best as we saw earlier it requires less operations to reach the same noisiness. I'm not sure why lookup multiply has so much higher difference error, it is practically the same code as multiply but with an added lookup. I guess the small lookup buffer size could be counter productive, it retrieves old, less multiplied values and that results in less noise than just multiplying the last state. These graphs are nice to have though, it confirms if we're trying to make a PRNG function with small operation count we want to use only multiply operations. Now keep in mind these are just the average errors across many generated functions. A larger value doesn't mean you will never generate a function with low error using the operations, but it is less likely.

Automation
To bring it all together we will automate the PRNG generation to meet our desired error thresholds. All the hard parts are already programmed, we just need to tie it together in a loop that generates, tests, repeats. To start let's create the class that's going to hold all the generation settings as well as the current state. Add the following code below.
You can see most of the arguments are the same as other functions. The new options maxValueError, maxDiffError and attemptCount determine when the autogeneration stops and the max amount of times it can run. Auto generating is incredibly simple, call GenPRNG to generate a PRNG, run TestPRNG to test it, use TestError to get the error and measure how far it is from the maxValueError and maxDiffError thresholds. We keep track of the PRNG with the lowest error to give us the best PRNG even when we fail to meet the thresholds. When we generate a decent PRNG we will want to save the code to reuse it later, we're going create a function SavePRNG that returns the PRNG as a JSON string and LoadPRNG which loads a JSON string into prngCode. Once we're done we display a message and output the PRNG code using SavePRNG to be reused later. We also need to terminate the WebWorker otherwise the memory won't be free'd. Insert the main autogeneration loop code.
Finally we have to kick off and start the loop, we will reset the state in autoGenConfig resetting attempt and bestError. We will also make sure the best buffer has enough space for the code generated by the config, then we start the loop by running AutoGenLoop. We're also going to make a function for stopping the auto generation, it will load in the best found PRNG so we can save it. Insert the code below.
To start auto generating a PRNG we can call AutoGenPRNG passing in a AutoGenConfig, run the code below in the console to generate a 5 operation 32-bit PRNG.
You can save the PRNG as JSON to load back into the generator or you can save the Javascript code using ToCodeJavascript.

Code
You can download the finished code below. Open the file in a browser and call the functions via the console to use it.
If the file opens in your browser, right click the page and use 'Save Page As' to download the .html.
Download PRNGG.html

In the file you will find I've added a few more code generation functions, ToCodeC, ToCodeC1, ToCodeGLSL and ToCodeGLSL1 will allow you to generate C and GLSL code. The 1 versions of the functions are designed for prngSize=1 and stateBufSize=1 functions that input and output a single uint32.

I've also auto generated some PRNG functions to use, see the table below.

Name	Bits	Op Count	Error	JSON	Javascript	C
TinyMulRnd32	32	3	3.84%	Download	Download	Download
ThinRnd32	32	3	3.99%	Download	Download	Download
ThinRnd64	64	4	3.96%	Download	Download	Download
FatRnd64	64	32	3.98%	Download	Download	Download
ThinRnd256	256	2	4.37%	Download	Download	Download

Error is calculated with 1e4 iterations, 100/prngSize difference range.